Distance vs Displacement
Distance vs Displacement
Learning Objectives
Students will;
Understand the importance of taking careful measurements.
Understand the importance of accurately recording data, including units.
Understand the advantage of being able to verify a quantity using distinct methods.
Learn the difference between vector and scalar quantities.
Learn the difference between distance and displacement.
Demonstrate the ability to use trigonometry to calculate displacement vectors.
Introduction
One of the most important lessons that you are likely to encounter when studying physics is on the difference between distance and displacement. This is the topic that many physics teachers use to introduce students to the concept of vector and scalar quantities. This early lesson is extremely important, because the tricks that you learn to use with displacement vectors will work again with other vector quantities, such as; velocity, acceleration and force. That means that the skills and terms that you are being introduced to now will be used for months to come. If you learn this lesson well, it will help set you up for success in physics.
Important Vocabulary
Scalar Quantity – a Scalar quantity, sometimes simply called “a scalar” for short, is a quantity that can be completely described with numbers and units. You don’t include a direction when reporting a scalar quantity. For example, if you ask someone how old they are, you are expecting a number and a unit as a response, although the unit of “years” might be assumed in most cases. Age is a scalar quantity, as you would not include a direction when reporting age.
Distance – We may all know what distance is, but it can be very hard to define. You might think of it as the amount of space between two points. If we walk in a nonlinear path, the distance we travel is the measure of the sum of the space that we moved through. Distance is a scalar quantity, because we aren’t required to indicate a direction. If you asked your friend how far he ran in track practice, you aren’t expecting him to specify the direction he ran. You are expecting a response that includes numbers and units, such as, “5 miles.”
Vector Quantity – A vector quantity, sometimes simply called “a vector” for short, is a quantity that requires a number, units, and a direction in order to be described. Physics deals with several vector quantities and they can all be represented graphically with arrows, as arrows can show direction. An example of a vector quantity would be force. When an engineer is studying forces on a bridge, the directions of the forces matter. You can’t determine the net (overall) force on an object without knowing the directions of the individual forces acting on it.
Displacement – Displacement in the change in an object’s position, including the direction of the change. The requirement to include a direction in the description of a displacement makes displacement a vector quantity. There are several ways to indicate the direction of a vector quantity in physics. Sometimes, we use arrows to indicate the magnitude and direction of a vector quantity graphically. Sometimes, when a vector is limited to one axis of direction, we use plus and minus signs to indicate direction. Sometimes, it is necessary to indicate direction with compass headings, such as, “4.5 meters and 17 degrees south of west.”
Magnitude – The term magnitude takes on an important meaning in physics, with regards to vector quantities. When we talk about the “magnitude of a vector quantity”, we are ignoring the direction, temporarily. If a question asks you for the magnitude of a displacement, the questioner is alleviating you of the requirement of reporting direction. In some cases, the magnitude of a displacement will be equal to the distance traveled, but each of these cases involves traveling in a straight line.
Component Vectors – Component vectors can be thought of as “parts” of a vector. For example, if a quarterback throws a football upwards and forwards, we can talk about the initial velocity of the football, which would be in both the upwards and forwards directions. However, we might also be interested in how fast the football is initially going upwards and how fast the ball is initially moving forwards. These vector quantities, represented by the red vectors in the image below, can be considered as “parts” or component vectors of the total initial velocity.
Resultant Vector – A resultant vector can be thought of as the “vector sum” of two or more component vectors. For example, let’s suppose that you walk 6.0 meters to the north, turn and walk 7.0 meters to the east and then turn and walk 6.0 meters to the south. Each “leg” of your total trip would be considered component vectors, represented by the blue arrows in the image below, of your trip. However, at the end of your journey, you are now 7.0 meters east of your starting position, so that is your resultant displacement. The vector sum of your displacement, represented by the purple arrow below, is 7.0 meters to the east.
Tip-to-Tail Method – Graphically, vectors can always be “moved”, as long as you don’t change the length or direction of the arrow. The tip-to-tail method of vector addition involves moving component vectors, if necessary, so that the “tip” of the first component vector touches the “tail” of the next component vector. This process is repeated until all of the component vectors are laid out “tip-to-tail”. The resultant vector is then drawn from the tail of the first component vector to the tip of the last component vector. If you are required to subtract a component vector, you can flip that component vector over by 180 degrees and then add this reflected vector with the tip-to-tail method.
Scenario
Now that we have a common set of terms to work with, let’s put our knowledge to practice with fun scenario.
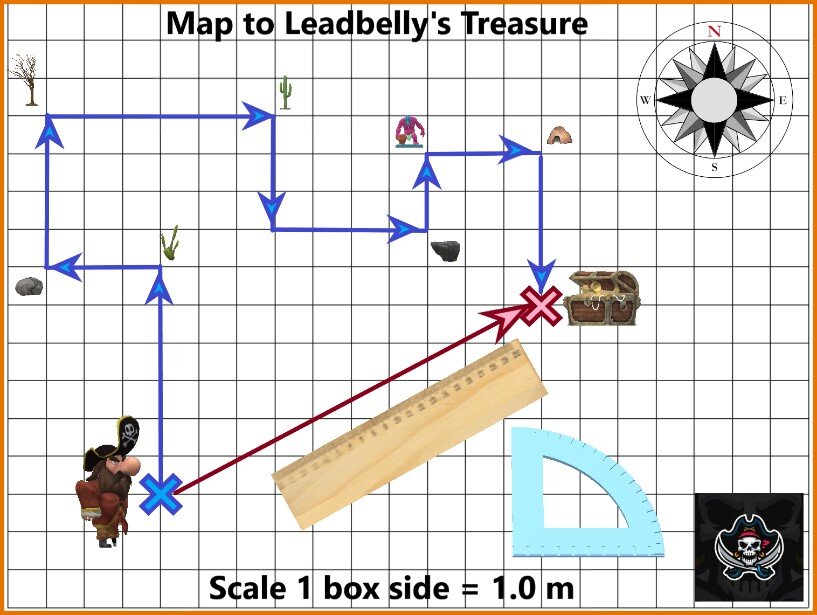
Salty Patrick McKenna has a plan that could make him the richest pirate captain on the seven seas! While the other Captains are filling their crews with; scoundrels, scamps and scallywags, armed with cutlasses, Captain McKenna is manning his ship with science scholars, armed with rulers, protractors and a knowledge of physics! Do you and your lab partner have what it takes to become part of Salty Pat’s crew?
Captain McKenna’s Plan - Every pirate worth his salt knows how to read a treasure map. You find the starting position on the map and follow the arrows to the treasure. The arrows don’t lead you directly to the treasure, but where’s the fun in that? These maps typically lead pirates on a merry chase around the landscape, often covering quite a distance, before bringing the reader to the treasure.
Captain McKenna, however, realizes that if he draws a displacement vector directly to the treasure, he can get to the prize by covering less distance in almost all cases. He will need two pieces of important information to use the new map that he created. He will need to know;
The magnitude of the displacement, which is the shortest distance between where he starts and where he wants to end up.
The direction that he must travel measured with a compass heading. For example, 32.0 degrees north of east.
Fortunately, Captain McKenna knows two methods for getting this information.
Method 1 - The Graphical Method
You can measure the length of the displacement vector with a meter stick or ruler, and then hold the meter along the lines on the graph paper to apply the scale. It is important to note that the diagonals of a square are longer than the side, so take care with the measurements. Also, pay attention to the accuracy of the instrument you are measuring with. Remember, you must take one and only one estimated digit when taking q measurement in science.
You can determine the angle for the direction of the displacement vector using a protractor. Be sure to measure the angle between the displacement vector and one of the compass headings (north, south, east or west). As indicated by the image of a compass in the picture above, we consider the top of the page to be north and the right of the page to be east.
Method 2 – The Trigonometry Method
In some cases, the graphical method is the only method for determining the displacement. This will be true when you can’t create a triangle out of the displacement vector and two other lines that are perpendicular to each other. Fortunately, examples like these are very easy, as shown below.
In the above image, the displacement would be 7.0 m north, based on the scale of 1.0 m per box side.
In more complex scenarios, you can take the displacement vector and turn it into the hypotenuse of a right triangle. The other sides of this right triangle must represent the displacement along two axes that are perpendicular to each other.
Now, you can find the length of the other two sides of the triangle by counting the number of squares they cover and applying the scale. You can find the magnitude of the displacement vector using the Pythagorean Theorem.
*Note – our scale is only accurate to 2 significant digits, so we round to 2 significant digits
To find the direction of the displacement vector, use the inverse tangent function, because you should know the lengths of both the opposite and adjacent sides of the triangle. Include the compass direction that you are measuring away from in your description of the direction.
Be sure that your calculator is in degree mode.
Putting that all together we would report our displacement at 11 m at 27 degrees north of east.
How do we know to call the direction of the displacement vector as “north of east” rather than “east of north”? Because the actual displacement vector is pointing in a direction that is measured, “away from east” in a northern direction, we would record our displacement as 11 m at 27 degrees north of east. This seems to be the part of the description of a vector that many of my students struggle with.
When you draw the displacement vector, always draw it as an arrow, not just a line. Point the arrow in the direction from the starting point to the end point. Then, create the rest of the right-triangle with arrows, as shown in the image below. Now, you will want to describe the angle in between the hypotenuse and the adjacent side to the angle. You will notice that the adjacent side is the arrow that points to a compass direction, say “east”, so that becomes the reference that the angle is measured away from.
Let’s do one more complete example. This time, why don’t you try to complete all of the work on your own and then just check my answer?
Finding the distance is the easy part. All we need to do is count the number of square-sides that the blue arrows pass through and apply our scale of 1.0 m per side. I get 7.0 meters when I apply the scale.
To find the magnitude of the displacement, I first draw my displacement vector as an arrow, from the initial position to the final position. I don’t need to draw arrows to complete the right-triangle, because this simple example already has component vectors that we can make use of.
We then use the Pythagorean theorem to determine the magnitude of the displacement and the inverse tangent to find the direction of the displacement. Since the adjacent side is pointing to the east, we write that last, as our reference direction.
Solution for example 3
I hope that you were able to get the same answer as me. Feel free to leave comments or questions below.
*The images in this lesson were created with Paint 3D